本系统中,立体定位系统作为主要数据输入通道,用于获取目标位置与机器人之间的相对位置。随后将这些现场实时空间信息融入先前建立的空间模型。期间需要确定前模型与实际的三维空间变换关系,即配准。
然后,机器人根据计算机辅助系统制定的运动计划进行运动操作。运动中,立体定位系统通过对机器人与目标空间位置的不断采集,结合机器人多轴控制器进行视觉控制。机器人控制系统如图1所示。框图中输入为机器人行走驱动伺服电机的反馈电流,输出为机器人的行走速度,由伺服调速实现。
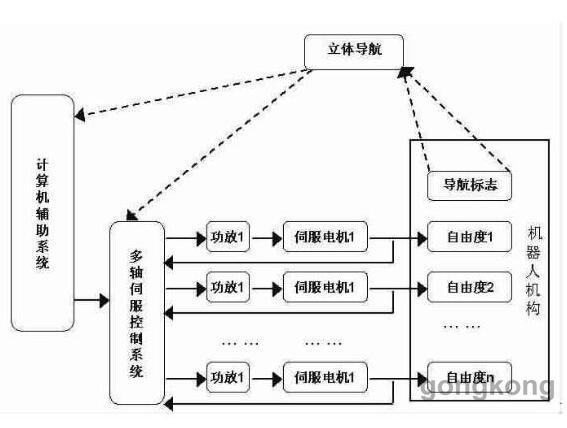
图1 机器人控制系统
本文设计的机器人为六自由度机器人:三个转动三个平动。机器人的六自由度协同完成空间运动。考虑到设计的机器人属于小型机器人,希望尽量减轻重量。这样一来,由于刚度下降而要求限定机构整体负载,同时还要考虑机构高速运动时的稳定性。而且,该多自由度机构的刚度设计取决于运动的速度与方向。
2模糊神经网络
2.1控制系统结构
结合机器人定位系统构建控制系统结构如图2所示,将机器人位置作为被控制量。
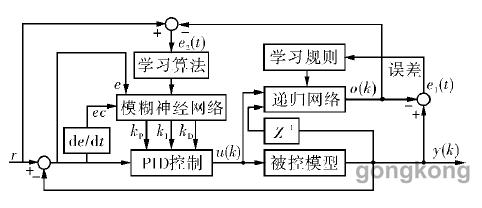
图2 模糊神经PID控制结构图
图中e和ec分别为误差和误差变化率,输入r为机器人位置,输出y为机器人实际输出。
2.2 模糊神经网络的结构
该模糊神经网络为4层,如图3所示。第l层为输入层;第2层为模糊化层;第3层为模糊推理层;第4层为输出层。模糊神经网络结构为2–6–6–3。
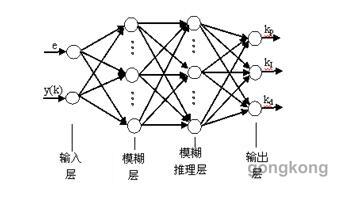
图 3. 模糊RBF神经网络的结构
(l)输入层。该层将输入误差e和系统实际输出y(k)作为下一层的输入。活化函数为:f(x)=x
因此本层的输出为e和y(k)
(2)模糊化层。活化函数即为该隶属度函数。因此,输出为:

其中,i=l,2;j=l,2,...6。cij和bij分别为高斯函数第i个输入变量的第j个模糊集合的隶属函数的均差和标准差。
(3)模糊推理层。将上层中的模糊量经过两两相乘,得到这一层的输出值。因此,本层的活化函数,即输出为:
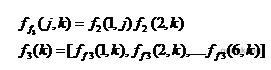
这里 k=l,2,3,4,5,6。
(4)输出层。这一层要输出的就是PID控制器的参数,本层的输出值就是将权值以矩阵乘的方式,乘以第3层的输出。因此,本层的输出为:
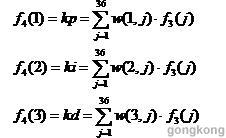
增量式PID控制的控制量为
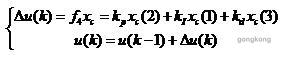
目标函数为:
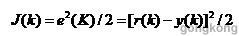
其中 r(k) 为期望输出。
2.3 鲁棒控制器
为保证闭环系统的稳定性和良好的控制效果,实时控制器由一个模糊神经网络控制器NNC和一个鲁棒控制器RC组成。这两个控制器的输出信号通过加权综合后,作为系统的控制输入[8-10],构成一个变鲁棒控制器u(k):
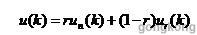
式中:un(k)为NNC的输出;ur(k)为鲁棒控制器的输出;γ为系统模型NNI的辨识精度,称为鲁棒因子。γ的表达形式为:
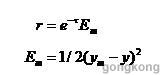
式中:τ为鲁棒因子的变鲁棒系数;Em为NNI输出与系统实际输出之差的平方。
3系统仿真研究
为了验证所提出的模糊神经网络控制算法的有效性,在MATLAB中创建模糊神经网络,利用隶属函数和模糊规则将抽象的模糊规则转化为模糊神经网络的训练样本,隐层采用在任意点可微的Tansig作为传递函数,输出层采用常用非负的Sigmoid函数。
采用常规PID控制和模糊神经网络控制时,系统阶跃信号的响应曲线。图3为常规PID控制器和模糊神经网络控制器对正弦信号跟踪的误差响应曲线,通过对比可知:模糊神经网络控制器在动态性能方面明显优于常规PID控制器,可将正弦响应误差从0.02 rad降至0.001 rad。
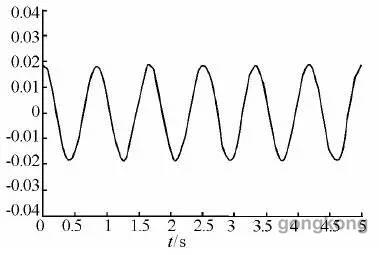
(a)PID 控制
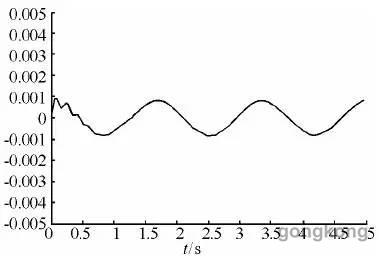
(b)模糊神经网络控制
图 3 系统正弦误差响应曲线